Инфофиз

Лабораторная работа № 3

Тема: "Сохранение механической энергии при движении тела под действием сил тяжести и упругости"

Цель: 1) научиться измерять потенциальную энергию поднятого над землей тела и упруго деформированной пружины;

            2) сравнить две величины—уменьшение потенциальной энергии прикрепленного к пружине тела при его падении и увеличение потенциальной энергии растянутой пружины.

Приборы и материалы: 1) динамометр, жесткость пружины которого равна 40 Н/м; 2) линейка измерительная; 3) груз из набора по механике; масса груза равна (0,100 ±0,002) кг; 4) фиксатор; 5) штатив с муфтой и лапкой.

Основные сведения.

Если тело способно совершить работу, то говорят, что оно обладает энергией.

Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.

Обозначается  Е Единица энергии в СИ  [1Дж = 1Н*м]

Кинетическая энергия – это энергия тела, обусловленная его движением.

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

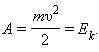
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела. 

Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй).

Ep = mgh

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину

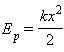, где k – жесткость пружины, х - абсолютное удлинение тела.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

A = –(Ep2 – Ep1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:

A = Ek2 – Ek1

Следовательно   Ek2 – Ek1 = –(Ep2 – Ep1)      или        Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.

Сумму E = Ek + Ep называют полной механической энергией.

Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.

Е = Ек + Еp = const 

Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.

Сила трения не является консервативной. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

Описание установки.

Для работы используется установка, показанная на рисунке. Она представляет собой укрепленный на штативе динамометр с фиксатором 1.

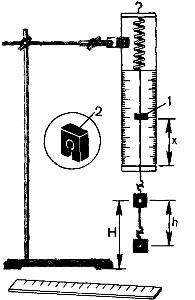
Пружина динамометра заканчивается проволочным стержнем с крючком. Фиксатор (в увеличенном масштабе он показан отдельно — помечен цифрой 2) — это легкая пластинка из пробки (размерами 5 Х 7 X 1,5 мм), прорезанная ножом до ее центра. Ее насаживают на проволочный стержень динамометра. Фиксатор должен перемещаться вдоль стержня с небольшим трением, но трение все же должно быть достаточным, чтобы фиксатор сам по себе не падал вниз. В этом нужно убедиться перед началом работы. Для этого фиксатор устанавливают у нижнего края шкалы на ограничительной скобе. Затем растягивают и отпускают.

Фиксатор вместе с проволочным стержнем должен подняться вверх, отмечая этим максимальное удлинение пружины, равное расстоянию от упора до фиксатора.

Если поднять груз, висящий на крючке динамометра, так, чтобы пружина не была растянута, то потенциальная энергия груза по отношению, например, к поверхности стола равна mgh. При падении груза (опускание на расстояние x = h) потенциальная энергия груза уменьшится на

Е₁=mgh

а энергия пружины при ее деформации увеличивается на

Е₂=kx²/2

Порядок выполнения работы

1. Груз из набора по механике прочно укрепите на крючке динамометра.

2. Поднимите рукой груз, разгружая пружину, и установите фиксатор внизу у скобы.

3. Отпустите груз. Падая, груз растянет пружину. Снимите груз и по положению фиксатора измерьте линейкой максимальное удлинение х пружины.

4. Повторите опыт пять раз. Найдите среднее значение h и х

5. Подсчитайте Е_1ср=mgh и  Е_2ср=kx²/2

6. Результаты занесите в таблицу:

7. Сравните отношение Е_1ср/ Е_2ср с единицей и сделайте вывод о погрешности, с которой был проверен закон сохранения энергии.

8. Ответьте на контрольные вопросы.

Контрольные вопросы.

Вариант выполнения измерений.