Инфофиз

Лабораторная работа № 2

Тема: Изучение закона сохранения импульса

Цель: экспериментально проверить справедливость закона сохранения импульса тел при прямом упругом соударении

Оборудование: 1. Два металлических шарика разной массы.

                        2. Рама для подвеса шариков.

                        3. Измерительная линейка.

Теория

   Величина, равная произведению массы материальной точки на ее скорость, называется импульсом.

p=mυ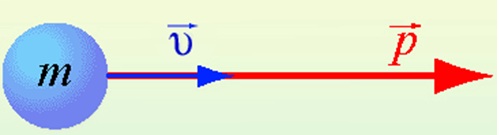  

p — импульс тела

m — масса тела

υ — скорость тела   

   Импульс тела направлен в ту же сторону, что и скорость тела.

   Единицей измерения импульса в СИ является 1 кг·м/с.

   Изменение импульса тела происходит при взаимодействии тел, например, при ударах.

   Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма.

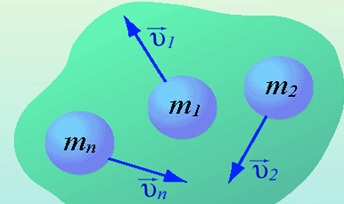
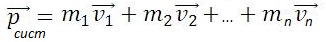
   Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. Замкнутая система – это система тел, которые взаимодействуют только друг с другом.

   Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

m₁, m₂ — массы взаимодействующих тел, кг

υ₁, υ₂ — скорости тел до столкновения, м/с

υ'₁, υ'₂ — скорости тел после столкновения, м/с

   Закон сохранения импульса можно сформулировать и так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления.

   Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближенно выполняется для этих процессов даже при наличии внешних сил, действующих на тела системы со стороны тел, не входящих в нее, т.к. за малое время внешние силы не успевают значительно изменить импульс системы.

   Под ударом в механике понимается кратковременное взаимодейс­твие двух или более тел,  возникающее в результате их соприкосно­вения (соударение шаров, удар молота о наковальню и др.). Самым простым является прямой (центральный) удар, то есть такой удар, при котором скорости соударяющихся тел до удара направлены по линии, соединя­ющей центры тел. При соударении взаимодействие  длится такой короткий промежуток времени (иногда измеряемый тысячными долями секунды) и возни­кают столь большие внутренние силы взаимодействия, что внешними силами можно пренебречь и систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.

   В зависимости от упругих свойств тел соударения могут проте­кать весьма различно. Принято выделять два крайних случая: абсо­лютно упругий и абсолютно неупругий удары.

   Абсолютно упругим называется удар, при котором после взаимодействия тела полностью восстанавливают свою форму. Таких ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел. Однако для некоторых  тел, например стальных закаленных шаров, потерями механической энергии при столкновении можно пренебречь и считать удар абсолютно упру­гим. В случае центрального абсолютно упругого удара двух тел с массами m₁, m₂  и скоростями υ₁, υ₂  до удара и υ′₁, υ′₂ после удара можно записать закон сохранения импульса тел:

   Абсолютно неупругим называется удар, при котором после соп­рикосновения тел они не восстанавливают полностью свою форму, со­единяются вместе и движутся как единое целое с одной скоростью. При этом ударе часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). Столкновение двух шаров из пластилина, когда после столкновения шары слипаются и движутся вместе, является примером абсолютно неупругого удара. В случае центрального абсолютно неупругого удара двух тел с массами m₁, m₂  движущихся со скоростями υ₁, υ₂  до удара и υ′ после удара можно записать законы сохранения импульса тел:

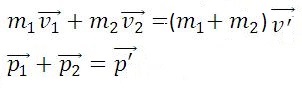
   Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:

1. Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.
2. Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике - при забивании свай, ковке металлов и т.д

Описание работы

Установка состоит из двух стальных шаров, на длинных подвесах и измерительной линейки под шарами. Центры масс соприкасающихся шарв лежат на одном уровне от точки подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно произвести прямой (центральный) удар шаров.

Если до столкновения один из шаров покоился υ₂=0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:

m₁∙υ₁= m₁∙υ′₁ + m₂∙υ′₂ 

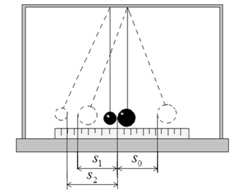
   рис. 2

   Для определения скорости первого шара υ₁ до удара  и скоростей шаров υ′₁ и υ′₂ после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его кинетической энергии при ударе 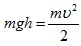, отсюда .

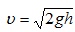   Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис.3,а).

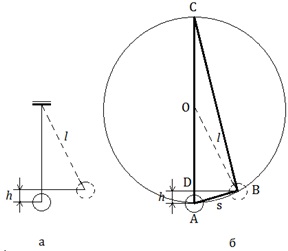
рис. 3

Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2l и своей проекцией на гипотенузу АD  (рис.3,б):  АВ²=АС·AD то есть 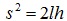, откуда 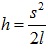. Следовательно, величины скоростей можно выразить так: 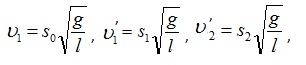где S₀,  S₁ - максимальные отклонения первого шара до и после удара; S₂ - максимальное отклонение второго шара после удара.

Запишем уравнение закона сохранения через выражения скоростей:

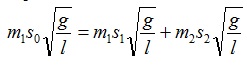  или  m₁∙S₀= m₁∙S₁ + m₂∙S₂.

Таким образом, проверка закона сохранения импульса в данной работе сводится к проверке справедливости последнего уравнения.

 При малых углах отклонения шара от положения равновесия S₀,  S₁ и S₂ можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.

Выполнение работы.

1. Перенесите рисунок 2 в отчет по работе.

2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:

Контрольные вопросы

1. Что называется импульсом материальной точки? По какой формуле он находится? В каких единицах он измеряется?

2. Импульс – величина векторная или скалярная?

3. Запишите формулу и формулировку закона сохранения импульса.

4. При каких условиях выполняется закон сохранения импульса?

5. Какое соударение называется абсолютно упругим?

6. Для каких видов соударений выполняется закон сохранения импульса?

Вариант выполнения измерений.

1. Определяем массы шариков m₁ и m₂  при помощи динамометра (или весов) и записываем в таблицу:

m₁=62 г

m₂=27,5 г

2. Отклоняем большой шар от положения расновесия на 3 см и отпускаем его. 

S₀=3 см=30 мм

Замечаем его максимальное отклонение после удара. Повторяем опыт 5 раз, находим среднее значение отклонения и записываем в таблицу S_1ср.

S₁=13мм   S₁=15мм   S₁=18мм    S₁=14мм   S₁=16мм

S_1ср=(13мм+15мм+18мм+14мм+16мм)/5=15,2 мм

3. Повторяем этот же опыт, но теперь замечаем после удара отклонение шара меньшей массы. Повторяем опыт 5 раз, находим среднее значение и записываем в таблицу S_2ср.

S₂=31мм   S₂=34мм   S₂=36мм    S₂=35мм   S₂=32мм

S_2ср=(31мм+34мм+36мм+35мм+32мм)/5=34мм

4. Повторяем опыт, отклоняя шар большей массы на 4 см и 5 см. 

S₀=4 см=40 мм

S₁=18 мм   S₁=19 мм   S₁=23 мм    S₁=22 мм   S₁=18 мм

S_1ср=(18 мм+19 мм+23 мм+22 мм+18 мм)/5=20 мм

S₂=43 мм   S₂=44 мм   S₂=46 мм    S₂=47 мм   S₂=45 мм

S_2ср=(43 мм + 44 мм + 46 мм + 47 мм + 45 мм)/5=45 мм

S₀=5 см=50 мм

Результаты измерений записываем в таблицу.