Инфофиз

Тема 3.2. Законы движения небесных тел. Определение расстояний и размеров тел в Солнечной системе.

3.2.1. Законы движения небесных тел.

Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером (1571—1630) и стали первыми естественнонаучными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие ученые вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой— окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.

В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного еще Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников Иоганн Кеплер и т. д.

Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих ее положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведенными его учителем Тихо Браге.Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Для того чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.

Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение  α₁, которое выражается углом Т₁М₁ где Т₁ — положение Земли на орбите в этот момент, а М₁ — положение Марса. Очевидно, что спустя 687 суток (таков звездный период обращения Марса) планета придет в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости ее орбиты. Земля в этот момент находится в точке Т₂, и, следовательно, угол T₂M₁ есть не что иное, как прямое восхождение Марса — α₂. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил еще целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.

Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этомрадиус-вектор планеты за равные промежуткивремени описывает равные площади.Впоследствии эта закономерность получила название второго закона Кеплера.

Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиус-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АА₁ ВВ₁ и СС₁ — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.

Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает ее скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.

Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений:     1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8′; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.

Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

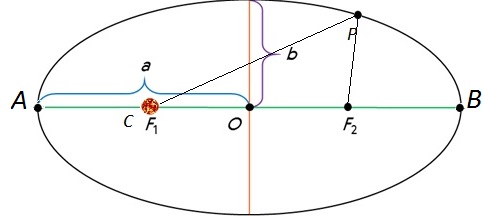
Как известно, эллипсом называется кривая, у которой сумма расстояний от любой точки Р до его фокусов есть величина постоянная. На рисунке 3.6 обозначены: О - центр эллипса; F и F₁ — фокусы эллипса; АВ — его большая ось. Половина этой величины (а), которую обычно называют большой полуосью, характеризует размер орбиты планеты. Ближайшая к Солнцу точка А называется перигелий, а наиболее удаленная от него точка В — афелий. Отличие эллипса от окружности характеризуется величиной его эксцентриситета: е = OS/OA. В том случае, когда эксцентриситет равен О, фокусы и центр сливаются в одну точку — эллипс превращается в окружность.

Примечательно, что книга, в которой в1609 г. Кеплер опубликовал первые два открытых им закона, называлась «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс...».

Оба этих закона, опубликованные в 1609 г., раскрывают характер движения каждой планеты в отдельности, что не удовлетворило Кеплера. Он продолжил поиски «гармонии» в движении всех планет, и спустя 10 лет ему удалось сформулировать третий закон Кеплера.

Квадраты звездных периодов обращения планет относятся между собой, как кубы больших полуосей их орбит.

Формула, выражающая третий закон Кеплера, такова:

где Т₁ и Т₂ — периоды обращения двух планет; а₁ и а₂ — большие полуоси их орбит.

Вот что писал Кеплер после открытия этого закона: «То, что 16 лет тому назад я решил искать, <...> наконец найдено, и это открытие превзошло все мои самые смелые ожидания...»

Действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя при этом уже известные периоды их обращения вокруг Солнца. Не нужно определять расстояние от Солнца каждой из них, достаточно измерить расстояние от Солнца хотя бы одной планеты. Величина большой полуоси земной орбиты — астрономическая единица (а. е.) — стала основой для вычисления всех остальных расстояний в Солнечной системе.

Пример решения задач

Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?