Уравнение движения тела, брошенного под углом к горизонту
Движение тела, брошенного под уголом к горизонту можно представить как сумму двух прямолинейных движений: равномерного вдоль горизонтальной оси x с начальной скоростью v0 и равнопеременного вдоль вертикальной оси y без начальной скорости с ускорением, равным ускорению свободного падения g.
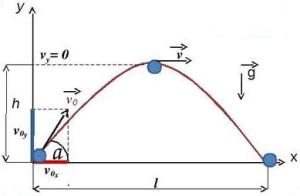
Системы кинематических уравнений для прямолинейного движения в проекциях на выбранные оси будут иметь вид
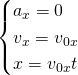
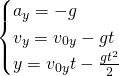
Проекции начальной скорости на оси координат соответственно равны:
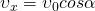 - проекция начальной скорости на ось x
- проекция начальной скорости на ось x
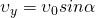 - проекция начальной скорости на ось y
- проекция начальной скорости на ось y
Так как рассматривается движение тела вдоль оси Х и вдоль оси Y, то уравнение движения тела, брошенного под углом к горизонту это будет система из двух уравнений. Движение вдоль оси Х равномерное, проекция скорости на ось Х не изменяется со временем, поэтому первая формула в системе уравнений - формула координаты при равномерном прямолинейном движении. Движение вдоль оси Y равноускоренное с ускорением свободного падения, проекция скорости на ось Y изменяется со временем, поэтому вторая формула в системе уравнений - формула координаты при равноускоренном движении:
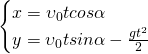
Решив систему мы получим
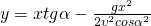
Обозначения:
x,y — координаты положения тела
v0 — начальная скорость тела
t — время движения тела
a — угол под которым было брошено тело
g — ускорение свободного падения
