Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
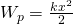
Потенциальная энергия упруго деформированного тела зависит от взаимного положения частей тела относительно друг друга, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины.
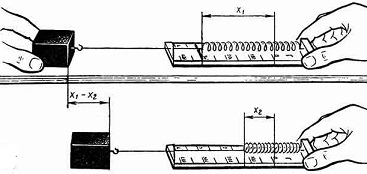
Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем потенциальную энергию растянутой пружины.
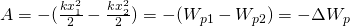
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Обозначения:
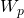— потенциальная энергия тела
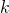— коэффициент жесткости (или просто жесткость) пружины
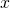— абсолютная деформация (удлинение или сжатие пружины)
A — работа, которую совершает растянутая пружина