Все вы в своей жизни наблюдали за тем, что тела, не имеющие опоры или подвеса, падают вниз. В чем причина такого падения? Конечно же в том, что на все тела у поверхности Земли действует сила тяжести.
Свободным падением тела называется движение тела только под действием силы тяжести.
Проведем мысленный эксперимент. Представьте, что одновременно начинают падение мяч, камень, лист дерева и перо птицы. В какой очередности упадут эти тела?
Первым упадут камень и мяч, затем перо и лист.
Почему? На перо и лист оказывает заметное влияние сила сопротивления воздуха, направленная против силы тяжести.
Падение тела не может считаться свободным, если сила сопротивления воздуха сравнима с силой тяжести.
Еще в конце XVI века знаменитый итальянский ученый Г. Галилей предположил, что все тела падают с одинаковым ускорением и опытным путем доказал, что это предположение верно.

Согласно биографии Галилео Галилея, написанной его учеником Винченцо Вивиани, в 1589 году Галилей провёл эксперимент, сбросив два шара различной массы (ядро и мушкетную пулю) со знаменитой падающей башни в Пизе, чтобы продемонстрировать, что время падения не зависит от массы шара. С помощью этого эксперимента Галилей якобы обнаружил, что тела упали практически одновременно, тем самым доказав, что в отсутствии сопротивления воздуха все тела падают на Землю равноускоренно и что в данной точке Земли ускорение всех тел при падении одно и то же.

Исаак Ньютон доказал справедливость выводов Галилео простым опытом.

В стеклянную трубку он поместил дробинку, пробку и перышко. Если резко перевернуть расположенную вертикально трубку, то быстрее всего упадет дробинка, за ней кусочек пробки и потом плавно опустится перышко. Если же из трубки откачать воздух и опять резко перевернуть её,то все три тела опустятся на дно одновременно.
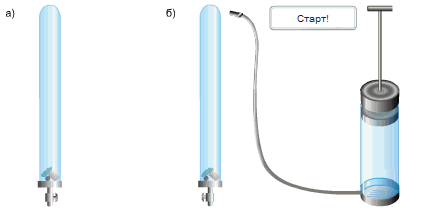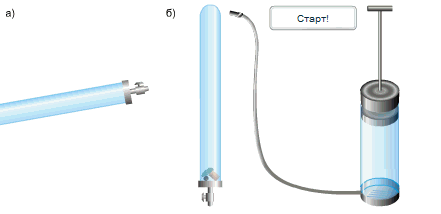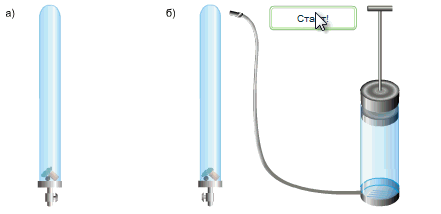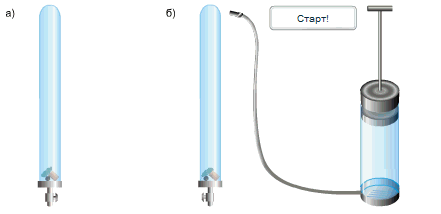
Какие выводы можно сделать из опыта Ньютона?
1. Тела падают с одинаковым ускорением.
2. Существует сила сопротивления воздуха
Ускорение, с которым тела падают на Землю, называется ускорением свободного падения.
Ускорение свободного падения - ускорение, сообщаемое телу, поднятому над Землей, силой тяжести.
Вектор ускорения свободного падения обозначается символом g.
g=9,8 м/с2≈10м/с2
Из закона всемирного тяготения: 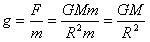
Ускорение свободного падения:
1) Всегда направлено по вертикали вниз
2) Не зависит от массы падающего тела
3) Зависит от географической широты. Так как Земля не шар, а эллипсоид вращения, т.е. радиус Земли на полюсе меньше, чем радиус Земли на экваторе.
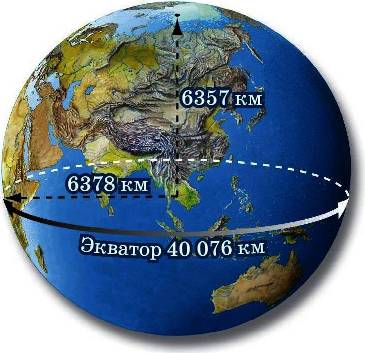
Поэтому сила тяжести и вызвемое ей ускорение больше на полюсе, чем на экваторе. g изменяется примерно от 9,83 м/с2 на полюсах до 9,78 м/с2 на экваторе. На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с2 или даже 10 м/с2.
4) Зависит от высоты над уровнем моря
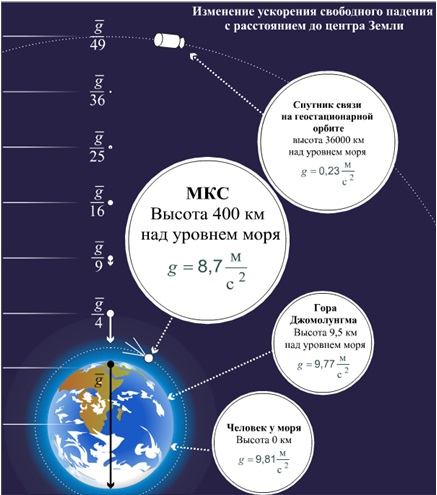
Рассмотрим несколько примеров движения тел под действием силы тяжести. При решении подобных задач очень важно правильно выполнить чертеж, на котором указать направление осей и всех векторных величин.
Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости.
Анализируем рисунок.
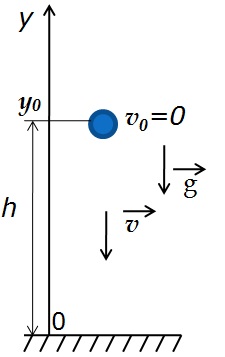
Свободное падение является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.
Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.
Тогда проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, с которой тело падало s=h, а проекция перемещения на ось y отрицательна: sy=-h
Начальная скорость движения равна нулю v0=0
Проекция конечной скорости на ось y отрицательна vу =-v
Начальная координата тела y0=h
Теперь работаем с формулами.
Проекция скорости на ось y при равноускоренном движении находится по формуле
vу=v0у+ayt
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и vу=-v, получаем -v=0-gt
Упростив выражение, получим формулу для нахождения скорости свободно падающено тела в любой момент времени:
v=gt
Проекция перемещения на ось y при равноускоренном движении находится по формуле
sу=v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и sу=-h, получаем -h=0-gt2/2
Упростив выражение, получим формулу для нахождения перемещения тела при свободном падении в любой момент времени:
h=gt2/2
Уравнение координаты при равноускоренном движении находится по формуле
y=y0+v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и y0=h, получаем y=h-gt2/2
То есть, формула для нахождения координаты тела при свободном падении в любой момент времени:
y=h-gt2/2
Как будет двигаться тело, брошенное вертикально вверх?
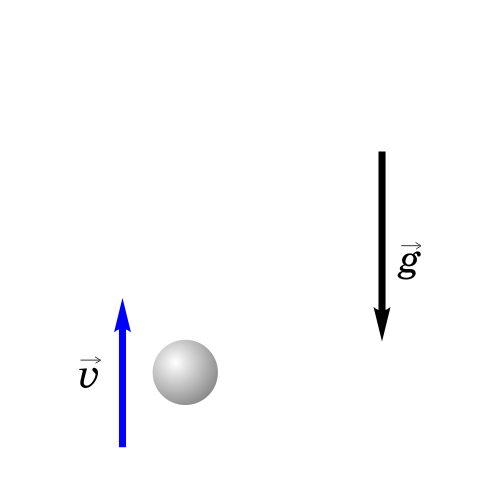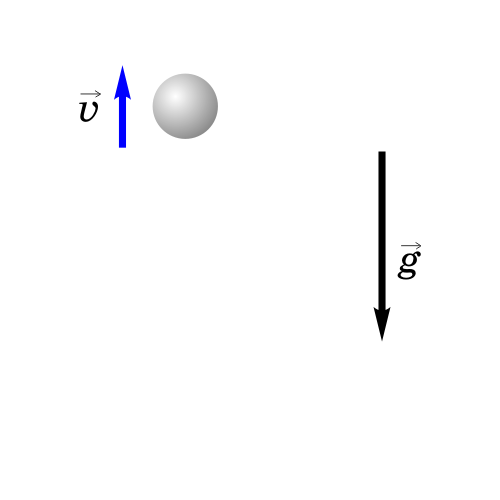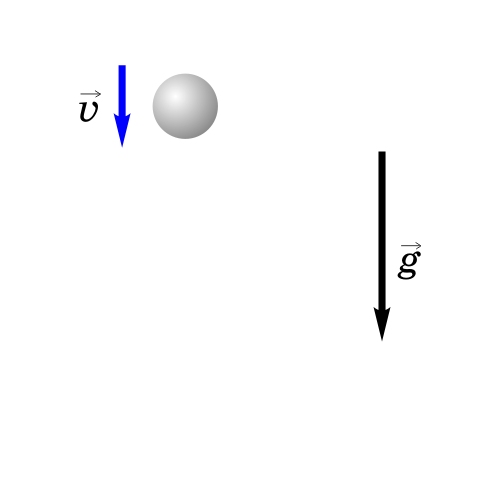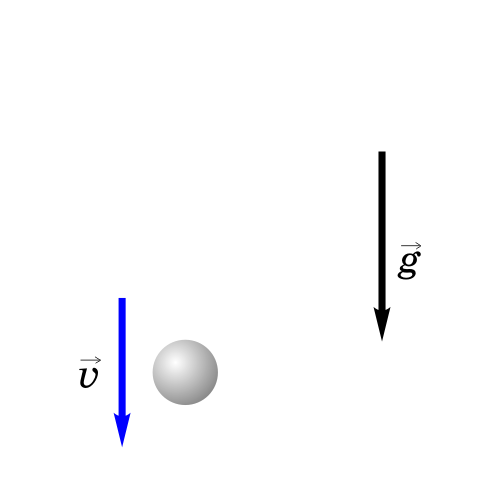
Если бросить тело вертикально вверх, то некоторое время оно будет двигаться вверх. Действующая на него сила тяжести направлена вниз и сообщает ему ускорение g, тоже направленное вниз. Поэтому скорость тела будет уменьшаться со временем и в некоторый момент она станет равной нулю, после чего тело начнет падать вниз с увеличивающейся скоростью.
Анализируем рисунок.
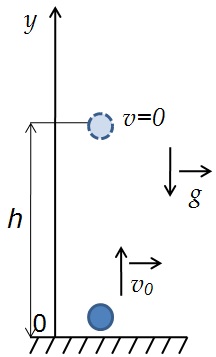
Движение тела, брошенного вертикально вверх тоже является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.
Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.
Тогда проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: sy=h
Проекция начальной скорости движения на ось y положительна v0y=v0
Конечная скорость в верхней точке равна нулю v =0
Начальная координата тела равна нулю y0=0, а конечная координата равна высоте, на которую тело поднимется y=h
Теперь работаем с формулами.
Проекция скорости на ось y при равноускоренном движении находится по формуле
vу=v0у+ayt
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 и vу=v, получаем, что скорость тела, брошенного вертикально в любой момент времени:
v=v0-gt
Если учесть, что в верхней точке v =0, получим 0=v0-gt
Упростив выражение, получим формулу для нахождения начальной скорости тела, брошенного вертикально:
v0=gt
Проекция перемещения на ось y при равноускоренном движении находится по формуле
sу=v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 и sу=h, получим формулу для нахождения перемещения тела, брошенного вертикально, в любой момент времени:
h=v0t-gt2/2
Уравнение координаты при равноускоренном движении находится по формуле
y=y0+v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 , y0=0 и y=h, получаем формулу для нахождения координаты тела, брошенного вертикально, в любой момент времени:
y=v0t-gt2/2
Как будет двигаться тело, брошенное горизонтально?
Если тело бросить горизонтально, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.
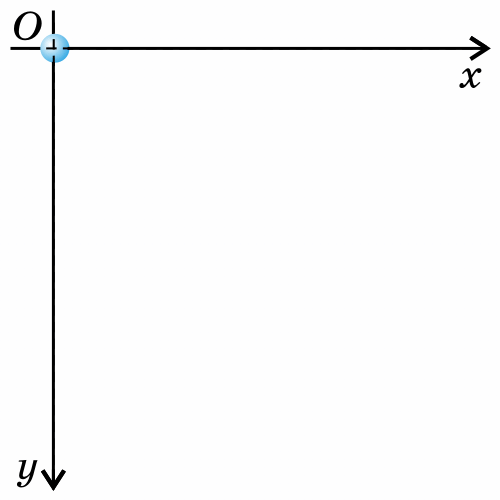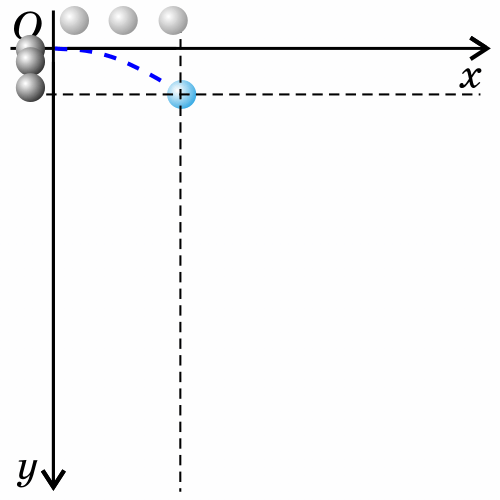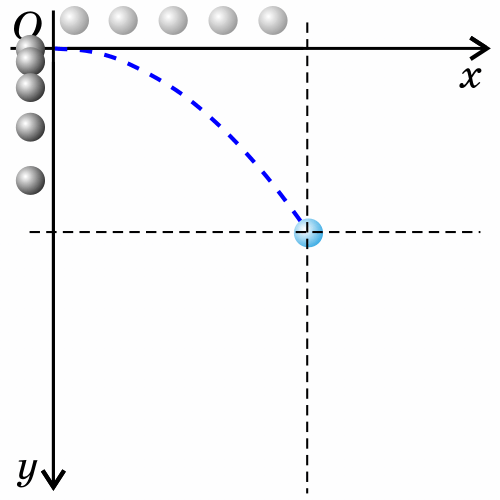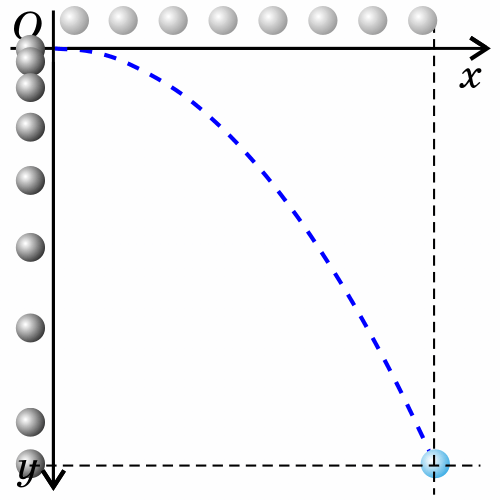
Такое движение тела рассматривают как два движения: по горизонтали - вдоль оси х, и по вертикали - вдоль оси y.
Анализируем рисунок.
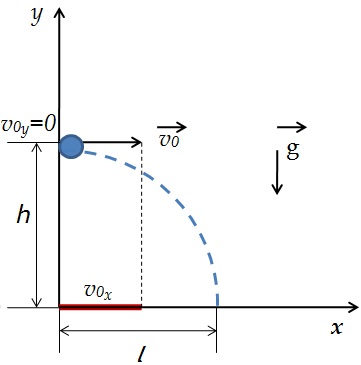
Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, с которой тело бросили s=h, а проекция перемещения на ось y отрицательна: sy=-h
Начальные координаты тела х0=0 y0=h
Проекция начальной скорости на ось х равна v0х=v0
Проекция начальной скорости на ось y равна v0y=0
Перемещение тела вдоль оси х это дальность полета sх=l=х-х0
Теперь работаем с формулами.
По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси х нужно пользоваться формулами, полученными для равномерного движения.
Уравнение скорости: v0x=v0=const
Уравнение перемещения (дальность полета): l=v0х·t= v0·t
Уравнение координаты: x= x0 + v0·t
По вертикали, т.е. вдоль оси y тело свободно падает с высоты h. Поэтому при рассмотрении движения вдоль оси y применимы формулы для свободного падения.
Уравнение скорости: v=g·t
Уравнение перемещения: h=g·t2/2
Уравнение координаты: y= y0-g·t2/2
Как будет двигаться тело, брошенное под углом к горизонту?
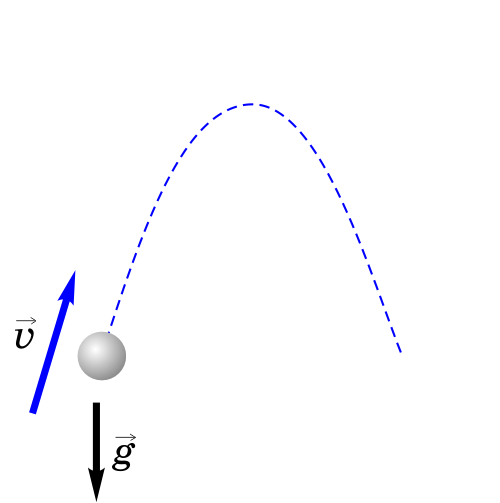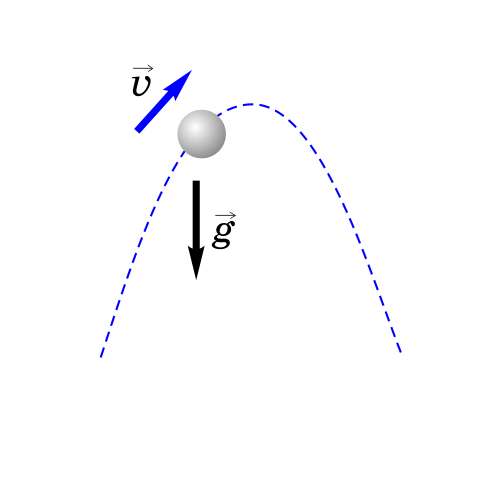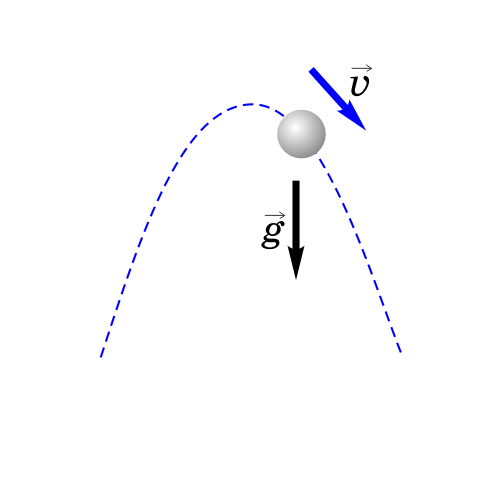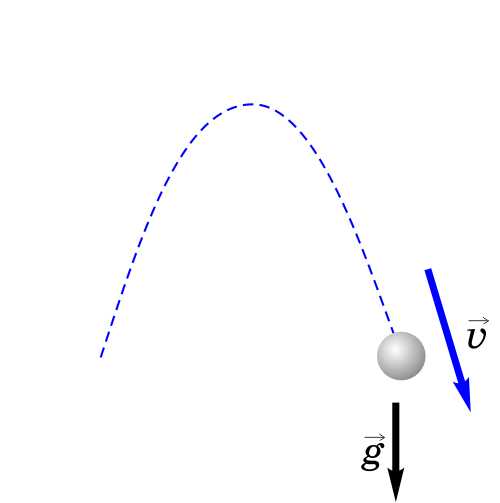
Если тело бросить под углом к горизонту, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.
Такое движение тела рассматривают как два движения: по горизонтали - вдоль оси х, и по вертикали - вдоль оси y.
Анализируем рисунок.
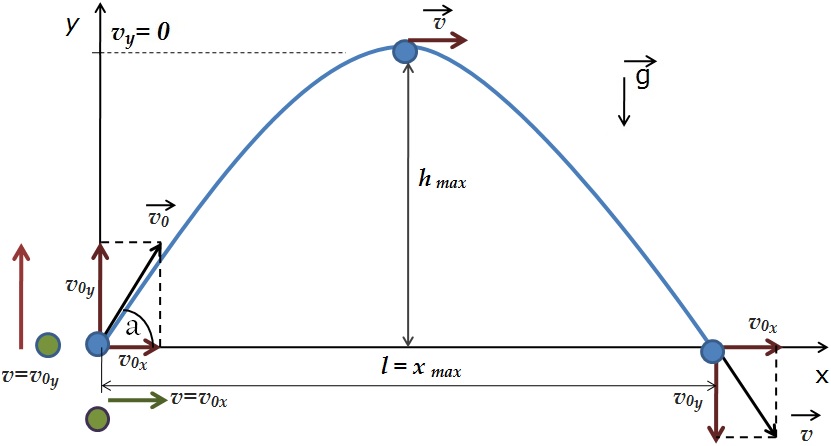
Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: sy=h
Начальные координаты тела равны нулю х0=0 y0=0
Проекция начальной скорости на ось х равна v0х=v0·cosa
Проекция начальной скорости на ось y равна v0y=v0·sina
h - максимальная высота, на которую тело поднимется. На этой высоте проекция скорости на ось y равна 0.
Перемещение тела вдоль оси х это дальность полета sх=l=х-х0
Теперь работаем с формулами.
По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения.
Уравнение скорости: v0x=v0·cosa=const
Уравнение перемещения (дальность полета): l=vxt= v0·cosa·t
Уравнение координаты: x= x0 + v0·cosa·t
По вертикали, т.е. вдоль оси y тело движется сначало равнозамедленно, подобно телу, брошенному вертикально вверх со скоростью, равной проекции начальной скорости на ось y, а затем равноускоренно (свободно падая).
Проекция ускорения на ось y gy= -g , проекция начальной скорости на ось y v0у=v0·sina, начальная координата y0=0
Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали.
Уравнение скорости: vy=v0·sina-g·t
Уравнение перемещения (максимальная высота полета): h=v0·sina·t-g·t2/2
Уравнение координаты: y= v0·sina·t-g·t2/2
Время полета в 2 раза больше времени подъема тела на максимальную высоту
t= 2·tmax = 2·v0·sina/g
Скорость тела находится по теореме Пифагора: ![]()
 .
.
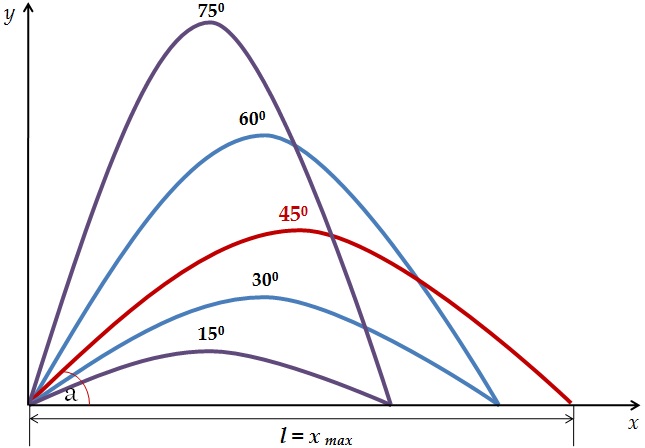
l = x max= v02·sin2a /g
Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=900, откуда a = 450
Для углов, дополняющих друг друга до 900 дальность полета одинакова.
