Лабораторная работа № 4.
Тема: Изучение зависимости периода колебаний нитяного маятника от длины нити.
Оборудование: штатив с перекладиной и муфтой, нить с петлями на концах, груз с крючком, линейка, электронный секундомер
Цель работы: состоит в экспериментальной проверке формулы, связывающей период колебаний маятника с длиной его подвеса.
Основные сведения
Рассмотрим колебания нитяного маятника, т.е. небольшого тела (например, шарика), подвешенного на нити, длина которой значительно превышает размеры самого тела. Если шарик отклонить от положения равновесия и отпустить, то он начнет колебаться. Сначала маятник движется с нарастающей скоростью вниз. В положении равновесия скорость шарика не равна нулю, и он по инерции движется вверх. По достижении наивысшего положения шарик снова начинает двигаться вниз. Это будут свободные колебания маятника.
Свободные колебания – это колебания, которые возникают в системе под действием внутренних сил, после того, как система была выведена из положения устойчивого равновесия.
Колебательное движение характеризуют амплитудой, периодом и частотой колебаний.
Амплитуда колебаний - это наибольшее смещение колеблющегося тела от положения равновесия. Обозначается А. Единица измерения - метр [1м].
Период колебаний - это время, за которое тело совершает одно полное колебание. Обозначается Т. Единица измерения - секунда [1с].
Частота колебаний - это число колебаний, совершаемых за единицу времени. Обозначается ν. Единица измерения - герц [1Гц].
Тело, подвешенное на невесомой нерастяжимой нити называют математическим маятником.

Период колебаний математического маятника определяется формулой: 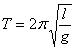 (1), где l – длина подвеса, а g – ускорение свободного падения.
(1), где l – длина подвеса, а g – ускорение свободного падения.
Период колебаний математического маятника зависит:
1) от длины нити. Период колебаний математического маятника пропорционален корню квадратному из длины нити ![]() . Т.е., например при уменьшении длины нити в 4 раза, период уменьшается в 2 раза; при уменьшении длины нити в 9 раз, период уменьшается в 3 раза.
. Т.е., например при уменьшении длины нити в 4 раза, период уменьшается в 2 раза; при уменьшении длины нити в 9 раз, период уменьшается в 3 раза.
2) от ускорения свободного падения той местности, где происходят колебания. Период колебаний математического маятника обратнопропорционален корню квадратному из ускорения свободного падения 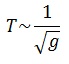 .
.
Тело, подвешенное на пружине называют пружинным маятником.

Период колебаний пружинного маятника определяется формулой 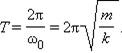 где m - масса тела, k - жесткость пружины.
где m - масса тела, k - жесткость пружины.
Период колебаний пружинного маятника зависит:
1) от массы тела. Период колебаний пружинного маятника пропорционален корню квадратному из массы тела 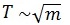 .
.
2) от жесткости пружины. Период колебаний пружинного маятника обратнопропорционален корню квадратному из жесткости пружины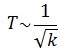 .
.
В работе мы исследуем колебания математического маятника. Из формулы 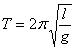 следует, что период колебаний изменится вдвое при изменении длины подвеса в четыре раза.
следует, что период колебаний изменится вдвое при изменении длины подвеса в четыре раза.
Это следствие и проверяют в работе. Поочередно испытывают два маятника, длины подвесов которых отличаются в четыре раза. Каждый из маятников приводят в движение и измеряют время, за которое он совершит определённое количество колебаний. Чтобы уменьшить влияние побочных факторов, опыт с каждым маятником проводят несколько раз и находят среднее значение времени, затраченное маятником на совершение заданного числа колебаний. Затем вычисляют периоды маятников и находят их отношение.
Выполнение работы.
1. Подготовьте таблицу для записи результатов измерений и вычислений:
|
l, м |
№ опыта |
N |
t, с |
tср, с |
Т, с |
ν, Гц |
|
l1 = |
1 |
30 |
|
|
|
|
|
2 |
30 |
|
||||
|
3 |
30 |
|
||||
|
4 |
30 |
|
||||
|
l2 = |
1 |
30 |
|
|
|
|
|
2 |
30 |
|
||||
|
3 |
30 |
|
||||
|
4 |
30 |
|
2. Закрепите перекладину в муфте у верхнего края стержня штатива. Штатив разместите на столе так, чтобы конец перекладины выступал за край поверхности стола. Подвесьте к перекладине с помощью нити один груз из набора. Расстояние от точки повеса до центра груза должно быть 25-30 см.
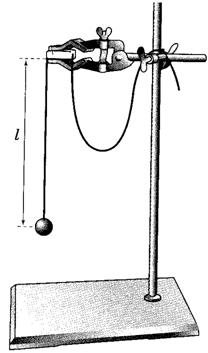
3. Подготовьте электронный секундомер к работе в ручном режиме.
4. Отклоните груз на 5-6 см от положения равновесия и замерьте время, за которое груз совершит 30 полных колебаний (при отклонении груза следите, чтобы угол отклонения не был велик).
5. Повторите измерение 3-4 раза и определите среднее время tср1=(t1+t2+t3+t4)/4
6. Вычислите период колебания груза с длиной подвеса 25-30 см по формуле 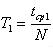 .
.
7. Увеличьте длину подвеса в четыре раза.
8. Повторите серию опытов с маятником новой длины и вычислите его период колебаний по формуле ![]() .
.
9. Вычислите частоты колебаний для обеих маятников по формулам ![]() и
и ![]() .
.
10. Сравните периоды колебаний двух маятников, длины которых отличались в четыре раза, и сделайте вывод относительно справедливости формулы (1). Укажите возможные причины расхождения результатов.
11. Ответьте на контрольные вопросы.
Контрольные вопросы
1. Что называют периодом колебаний маятника?
2. Что называют частотой колебаний маятника? Какова единица частоты колебаний?
3. От каких величин и как зависит период колебаний математического маятника?
4. От каких величин и как зависит период колебаний пружинного маятника?
5. Какие колебания называют собственными?
Вариант выполнения лабораторной работы.
Результаты измерений:
|
l, м |
№ опыта |
N |
t, с |
tср, с |
Т, с |
ν, Гц |
|
l1 = |
1 |
30 |
29 |
|
|
|
|
2 |
30 |
28 |
||||
|
3 |
30 |
28 |
||||
|
4 |
30 |
29 |
||||
|
l2 = |
1 |
30 |
53 |
|
|
|
|
2 |
30 |
54 |
||||
|
3 |
30 |
54 |
||||
|
4 |
30 |
54 |
