Квадратным уравнением называется уравнение вида ax2+bx+c=0, где x - переменная, a,b,c - постоянные (числовые) коэффициенты.
Алгоритм решения квадратного уравнения в общем случае:
1. Перевести все слагаемые в левую часть уравнения, упростить ее, получив уравнение вида ax2+bx+c=0
2. Вычислить дискриминант D.
Формула дискриминанта: D=b2-4ac
3. Вычислить корни уравнения x1 и x2.
Количество корней квадратного уравнения определяется по значению дискриминанта (D) :
D>0 - уравнение имеет 2 различных вещественных корня
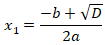 и
и 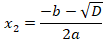
D=0 - уравнение имеет 1 корень
![]()
D<0 - корней нет
Частные случаи решения квадратного уравнения.
1. Если коэффициент при х четный, то вычисляется не дискриминант, а четверть дискриминанта:
![]()
В этом случае корни уравнения вычисляются по формуле:
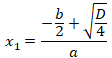 и
и 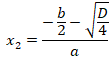
2. Для решения приведённых квадратных уравнений применяют теорему Виета.
Если в уравнении ах2+bх+с=0 первый коэффициент равен 1 (а=1), то уравнение называется приведенным квадратным уравнением.
Приведенное квадратное уравнение имеет вид x2+bx+c=0
Любое квадратное уравнение можно сделать приведенным, если его поделить на коэффициент a при х2.
Теорема Виета: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно третьему коэффициенту.
Если х1 и х2 - корни квадратного уравнения x2+bx+c=0, то
х1+х2=–b
х1·х2=с
Если х1 и х2 - корни квадратного уравнения ax2+bx+c=0, то
х1+х2=–b/а
х1·х2=с/а
3. Неполные квадратные уравнения.
а) Квадратное уравнение вида ax2=0
Корень уравнения:
x=0
б) Квадратное уравнение вида ax2+bx=0
Корни уравнения:
x1=0
x2=-b/a
в) Квадратное уравнение вида ax2+c=0
Корни уравнения зависят от с/a:
При с/a≥0
![]() и
и ![]()
При с/a<0 корней нет.
