В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания.
Электромагнитными колебаниями называют периодические взаимосвязанные изменения заряда, силы тока и напряжения.
Свободными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Вынужденными называются колебания в цепи под действием внешней периодической электродвижущей силы
Свободные электромагнитные колебания – это периодически повторяющиеся изменения электромагнитных величин (q – электрический заряд, I – сила тока, U – разность потенциалов), происходящие без потребления энергии от внешних источников.
Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур или колебательный контур.
Колебательный контур – это система, состоящая из последовательно соединенных конденсатора емкости C, катушки индуктивности L и проводника с сопротивлением R
Рассмотрим закрытый колебательный контур, состоящий из индуктивности L и емкости С.
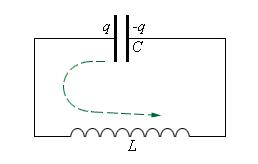
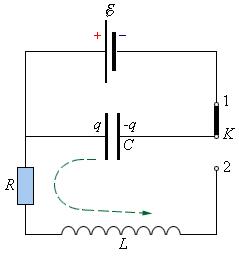
Чтобы возбудить колебания в этом контуре, необходимо сообщить конденсатору некоторый заряд от источника ε. Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер
Свободные электромагнитные колебания можно наблюдать на экране осциллографа.
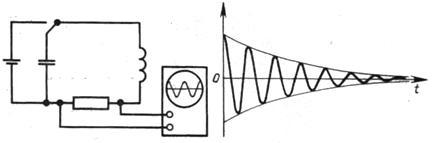
Как видно из графика колебаний, полученного на осцилографе, свободные электромагнитные колебания являются затухающими, т.е.их амплитуда уменьшается с течением времени. Это происходит потому, что часть электрической энергии на активном сопротивлении R превращается во внутреннюю энерги. проводника (проводник нагревается при прохождении по нему электрического тока).
Рассмотрим, как происходят колебания в колебательном контуре и какие изменения энергии при этом происходят. Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0).
Если зарядить конденсатор до напряжения U0 то в начальный момент времени t1=0 на обкладках конденсатора установятся амплитудные значения напряжения U0 и заряда q0 = CU0.
Полная энергия W системы равна энергии электрического поля Wэл:
![]()
Если цепь замыкают, то начинает течь ток. В контуре возникает э.д.с. самоиндукции
![]()
Вследствие самоиндукции в катушке конденсатор разряжается не мгновенно, а постепенно (так как, согламно правилу Ленца, возникающий индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Т.е. магнитное поле индукционного тока не дает мгновенно увеличиться магнитному потоку тока в контуре). При этом ток увеличивается постепенно, достигая своего максимального значения I0 в момент времени t2=T/4, а заряд на конденсаторе становится равным нулю.
По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля. Полная энергия контура после разрядки конденсатора равна энергии магнитного поля Wм:
![]()
В следующий момент времени ток течет в том же направлении, уменьшаясь до нуля, что вызывает перезарядку конденсатора. Ток не прекращается мгновенно после разрядки конденсатора вследствии самоиндукции (теперь магнитное поле индукционного тока не дает магнитному потоку тока в контуре мгновенно уменьшиться). В момент времени t3=T/2 заряд конденсатора опять максимален и равен первоначальному заряду q = q0, напряжение тоже равно первоначальному U = U0, а ток в контуре равен нулю I = 0.
Затем конденсатор снова разряжается, ток через индуктивность течёт в обратном направлении. Через промежуток времени Т система приходит в исходное состояние. Завершается полное колебание, процесс повторяется.
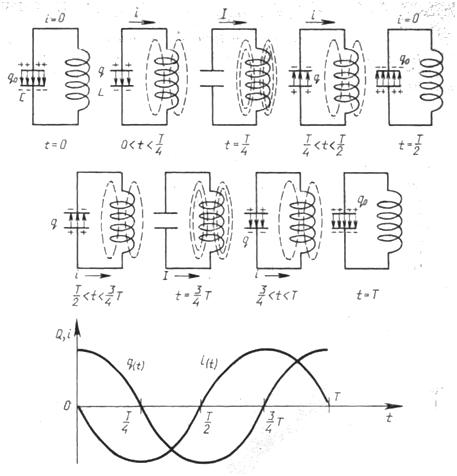
График изменения заряда и силы тока при свободных электромагнитных колебаниях в контуре показывает, что колебания силы тока отстают от колебаний заряда на π/2.
В любой момент времени полная энергия:
![]()
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается постоянной.
Свободные электрические колебания аналогичны механическим колебаниям. На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока I(t) и скорости груза υ(t) за один период колебаний.
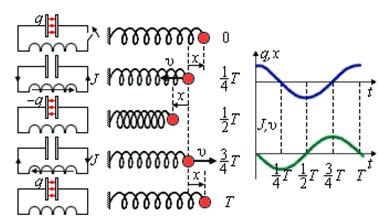
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
q(t) = q0cos(ωt + φ0)
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний ![]() и период колебаний
и период колебаний ![]() - формула Томпсона
- формула Томпсона
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.
Для колебаний заряда, напряжения и силы тока получаются формулы:
Для конденсатора:
q(t) = q0cosω0t
U(t) = U0cosω0t
Для катушки индуктивности:
i(t) = I0cos(ω0t + π/2)
U(t) = U0cos(ω0t + π)
Вспомомним основные характеристики колебательного движения:
q0, U0, I0 - амплитуда – модуль наибольшего значения колеблющейся величины
Т - период – минимальный промежуток времени через который процесс полностью повторяется
ν - Частота – число колебаний в единицу времени
ω - Циклическая частота – число колебаний за 2п секунд
φ - фаза колебаний - величина стоящая под знаком косинуса (синуса) и характеризующая состояние системы в любой момент времени.
